Subscribe to Blog via Email
Good Stats Bad Stats
Search Text
December 2024 S M T W T F S 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 -
Recent Posts
Good Stats Bad Stats
goodstatsbadstats.com
Wages, Simpson’s paradox and the complexity of statistical analysis
I spotted this good description of Simpson’s paradox in the trend data on wages over at the Inside-R blog today. Revolution Analytics did a good job explaining how Simpson’s paradox applies. At every education level median wages declined. However, for all people median wages have increased over the same time period. The reason for the difference is in the changes in the composition of the various groups over time.
The source article was at the New York Times. The New Statesman also gives another perspective explanation of what was going on utilizing the New York Times piece.
But where the New York Times creates some confusion was in saying “Low-Paid Workers Lose.” This implies that it is group of people who all lost out at an individual level. It is not until the very end of the piece that they clarify that they are not referring to the same people at both ends of the time period. But it is this point that is key to understanding what is happening. And it is at this point that the politicians take advantage of the statistics to make their points. They can say that workers at all education levels are losing out, and ignore the true situation.
Here what is likely happening is, particularly during the recession of the past few years, jobs that used to require only a high school diploma or some college now are occupied by those with a college degree. But the wages for the job have not changed to reflect the higher level of education of the job holder. As a result the median wages for those with college degrees has gone down.
The New York Times captured this phenomenon a couple of years ago in 2011 with an article titled “The Master’s as the New Bachelor’s.” They called it “Call it credential inflation.” With one person quoted as saying “Several years ago it became very clear to us that master’s education was moving very rapidly to become the entry degree in many professions.” That article goes on to claim without any real data that we are sending people to college who should not be there and do not need to be there for the jobs they end up with. That may be true, but we are also in a situation where many jobs require more skill than they used to. Many manufacturing jobs have moved from manual assembly of a product to operating the robotics that do the assembly. Both produce the same end product but the skill set required for the job has changed dramatically.
It is these kind of complexities that make dealing with number and statistics a challenging endeavor. It requires careful thought to understand what is the real story the statistics are telling us. It is all to easy to be led astray by looking at the numbers in haste or listing to someone tell a very smooth story.
Posted in Methodolgy Issues, The Media
Income Mobility
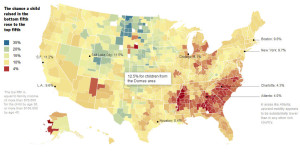This past week there were a number of stories on income mobility in the United States. The work these reports were based on was a paper titled: “The Economic Impacts of Tax Expenditures: Evidence from Spatial Variation Across the U.S.” out of Harvard and the University of California. Interestingly, based on the title, the main focus of the paper was on taxes and income mobility. However the published reports tended to ignore the tax angel and focused on income mobility as impacted by social conditions, segregation, and the availability of public transportation. The New York Times summed it with their piece “In Climbing Income Ladder, Location Matters” and the accompanying graphic which is shown at the right. Their graphic is much better than those I saw from the authors and from other sources. The New York Times frequently does a very good job with their graphics.
Before I go on let me commend the authors who have created a web site where anyone can view their paper and all of the associated data. It is rare indeed when authors provide that level of detail for the work they have done. That effort is much appreciated and the authors should be commended for making the data so easily available.
The study was based on tax data for parents and set of kids born in 1980 and 1981. The authors looked at where in the income distribution the parents were and where the children were in the income distribution years later. This was not a measure of income mobility for an individual but rather mobility over two generations. The question being considered was how well the children did relative to the parents. The New York times graphic and much of the reporting centered around one number. This was the probability that he child was in the top quintile given the parents were in the bottom quintile. The data for for 741 commuting zones is provided at the web site and is reflected in the graphic.
It is unfortunate that the focus was on specific areas. Looking at the New York times graphic the arc from South East Virgina to Western Mississippi where the children seemed to fare the worst by the metric that the authors used is very similar to what has been seen in other graphics.
First notice the graphic from a Census Bureau report showing Black population percentages by county. Notice the ark across the South where the counties have the higher proportion of Blacks than in the rest of the county matches the same arc seen in the income mobility graphic. This raises the question as the influence of race on upward mobility.
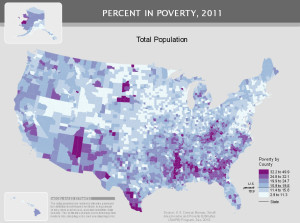
Next look at the graphic of poverty rates by county. That also was published by the Census Bureau. The same arc, this time of high poverty rates is seen in this graphic as in the previous two. Should we ask is poverty itself related to lower income mobility?
But the story is much more complex. There is lower income mobility in Ohio and Michigan than in other part of the county. But those two states do not show up as areas with higher Black population or higher poverty. Sure there are individual cites in those two states with high concentrations of Blacks and poverty. But the income mobility issue covers a much larger area than just those cites. Then there are areas of eastern Kentucky and West Virginia with high poverty rates but the income mobility is better than elsewhere. This tells us that the story may well vary by areas of the country. There is likely not just one reason for the differences in income mobility, but many reasons.
Complex situations like this are not easy for the media to deal with and require some difficult work for researcher to ferret out what is going on in the real world.
After examining some of the data the authors posted at the web site I think there are indications that the simple one number method for measuring income mobility has serious flaws. Looking at just the one number may be a good starting point. But the data set provides a much more robust set of number that ask for more answers and more research.
As a starting point I picked two commuting zones – Atlanta, GA and Pittsburgh, PA. Atlanta was picked as it had a low income mobility rate and was featured in many of the news reports. I picked Pittsburgh as it had one of the higher income mobility rates and I knew the city having lived there for six years. The data the authors provide show a poverty rate for Pittsburgh of 12.5% and for Atlanta of 9.9%. That makes Pittsburgh the poorer area on that metric. Pittsburgh was 7.0% Black, while Atlanta was 25.8% Black.
Using the data from the author’s web site the two tables below show the full transition matrix for the two areas. The numbers in the table reflect the probability that the child will move from a given quintile for the parent to a given quintile for the child. So these are actually conditional probabilities. Each column represents the probability that the child is in a particular income quintile given the parents income quintile. The New York Times article focused first on the probability of moving from the lowest(1st) quintile to the highest(5th) quintile. For Atlanta that number is 4.0%. For Pittsburgh that number is 10.3%.
These two tables change the entire perspective. Look closely the last two rows of both tables. Regardless of the parent’s income quintile the child’s probability of being in the top two quintiles of income in Atlanta are less that the probabilities in Pittsburgh. What was presented as being a poverty problem can now be seen as something that is happening at all income levels for the parents. Arguments like, race, segregation, and access to public transportation no longer have the same weight when all income groups are impacted.
What is going on? I don’t have an answer and would certainly caution about making conclusions based on just the data for two areas. Perhaps there is something going on with the passage of time that had impacted the two areas differently. Perhaps over the last few decades Pittsburgh has been more successful at attracting the higher paying jobs than Atlanta has been. That is why it is necessary to look at much more of the data, at more areas before coming to any hypothesis about what the differences mean. But clearly differences like that observed in these two tables need to be explained before there can be an understanding of what this data is showing us.
I see an interesting problem with many research papers devoted to the issue. But the paper these authors have put forth is a very good starting point.
| Parent’s Quintile | |||||
| Child’s Quintile | 1 | 2 | 3 | 4 | 5 |
| 1 | 31.0 | 24.2 | 19.7 | 16.7 | 15.0 |
| 2 | 36.8 | 31.9 | 22.5 | 20.7 | 15.1 |
| 3 | 19.3 | 22.0 | 22.1 | 20.5 | 17.3 |
| 4 | 9.0 | 14.0 | 18.5 | 21.2 | 22.4 |
| 5 | 4.0 | 8.1 | 14.3 | 20.9 | 30.2 |
| Parent’s Quintile | |||||
| Child’s Quintile | 1 | 2 | 3 | 4 | 5 |
| 1 | 31.7 | 22.1 | 15.6 | 11.1 | 10.1 |
| 2 | 23.9 | 20.6 | 17.4 | 14.0 | 11.7 |
| 3 | 19.3 | 21.4 | 21.1 | 19.7 | 16.3 |
| 4 | 14.7 | 19.4 | 22.8 | 24.5 | 23.7 |
| 5 | 10.3 | 16.5 | 23.2 | 30.6 | 38.1 |
Fish oil and prostate cancer
A week or so ago the media was telling us about a new study linking omega-3 and prostate cancer. The local news folks were suggesting that we might all want to do without those fish oil capsules. The story on CCN was headlined: Hold the salmon: omega-3 fatty acids linked to higher risk of cancer. The reports were based on the paper “Plasma Phospholipid Fatty Acids and Prostate Cancer Risk in the SELECT Trial published in the Journal of the National Cancer Institute.
Of course the health food industry did not like the study. The first criticism I heard was that it was a correlation study and thus in no way could show cause and effect. A full list of criticism from many sources is given in piece at Nutraingredients.com.
I managed to get a copy of the paper and after reading it over the last week have a number of issues with the work that was done. My bottom line is that I would ignore the claims that are being made. The study has a number of major shortcomings and problems that go well beyond the issue of being just a correlation study that cannot show cause and effect.
As a start the study did not ask or attempt the find out if those in the sample used fish oil. They measured omega-3 in the blood. I do not know the way the body digest and maintains omega-3 in the blood, but can envision that there are a number of reasons why the level would vary independent of how often or how much one used fish oil capsules or by varying their diet.
The people entered the study between 2001 and 2004 and the occurrence of prostate cancer was ascertained up to 2009. There was only one measurement of the level of omega-3 in the blood. This then implies a very short term effect of the omega-3 in causing an increased risk for prostate cancer. To claim that such an increased risk can be measured based on the level of omega-3 at one point in time is to say the least a bit dubious. Perhaps the fellow ate salmon the night before the test.
The problems do not stop there. The paper provides a detailed table of the demographics with several biomarkers for the sample. It is clear from the table the prostate cancer risk is associated with the body mass index, with race, with baseline PSA to name just three. Yet the study does not claim to take these factors into the model.
The authors created a control group for their tests. But because the cost of the tests were high they performed a subsample of those without prostate cancer. They did this by “matching men randomly selected for the subcohort from the set of men with blood samples available within the same age-race stratum. A ratio of 1:3 was used for black men and 1:1.5 for men of other races.” In simple terms they sampled the non black at twice the rate used for black men in creating the control group. A a result nonblacks are overrepresented in the control group relative to there presence in the prostate cancer group. No attempt is provided in the paper describing any efforts made to account for this imbalance.
Table 2 of the paper provides mean levels of omega-3 for those without cancer and those with cancer. For those without cancer the value is 4.48 with a confidence interval(95%) from 4.41 to 4.55. For those with cancer the mean is 4.66 with a confidence interval(95%) from 4.56 to 4.75). The means are clearly different. But that is the wrong viewpont. The proper perspective here is the overlap in the distributions of the value of the omega-3 level between the two groups. With an n=1364 in the no cancer group and n=834 in the cancer group there is clearly considerable spread in the distributions. The overlap in values between the two groups is substantial. The lesson here is look at both the variance and the mean not just the mean. In simple terms I would like to know what is the probability that someone with the cancer has a higher omega-3 value than did someone without the cancer.
Then there is table 3 witch shows relative risks of prostate cancer by level of omega-3. For levels under 3.68 they give a reference risk of 1.00. For levels between 3.68 and 4.41 the risk is 1.15(0.87 to 1.51). for levels between 4.42 and 5.31 the risk is 1.28(0.97 to 1.69). And for levels over 5.31 the risk is 1.43(1.09 to 1.88). The numbers in brackets give the 96% confidence intervals. At the bottom of the table section is noted Ptrend with a value of 0.007. No indication of how this value was calculated is provided. Given the size of the confidence intervals it is very hard to envision how a statistically significant trend line could have been obtained. But even if there is a trend all this shows is a correlation. It does not show a cause and effect.
I will ignore the study.
I am beginning to think it would be worthwhile creating a table of all the things that various papers and reports link to increased risk the things like cancer, diabetes, heart disease.
Posted in Data Quality, Don't Use the Mean, Statistical Literacy, The Media