Do you really know the number that accurately?

I was looking at the list of potentially hazardous asteroids at spaceweather.com yesterday. The site provides a variety of information on the state of the sun, aurora forecasts, on current and future comets, and at the bottom of the page they provide a table listing recent and upcoming earth-asteroid encounters. It is a neat and very useful/interesting site for those interested in such things.

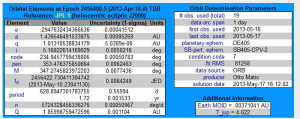I went on and looked at the details for one of the asteroids. These can be found by clicking on the asteroid name in the table. On of the neat things is that it provides a graphic of the orbit of the asteroids that one can play around with. They do the same thing when they provide information of current comments. It is a very neat feature of the site. But I was dismayed when I noted how accurately they show the orbit elements of the asteroid. Well, they don’t really claim to know the orbit with great accuracy, they just show the numbers as if they did know. The table at the right is the data for asteroid 2013 KA. The site is good in that is provides both the individual orbital elements and a measure of the accuracy each of those elements. But there is a serious disconect between the claimed accuracy and the accuracy that is shown for the individual orbital elements.

As an example they tell me that the semi-major axis of the orbit is 1.436546491533875. I get sixteen digits of accuracy. But then they tell me that the standard error on that number is 0.00085269. In short they only have the semi-major axis measured to an accuracy of about three decimal places. So why tell me the number to fifteen decimal places? Now the units of measurement here are astronomical units. An astronomical unit is approximately 93 million miles. So they know the number to about 9,300 miles. But they give me the number to an implied accuracy of about five thousandths of an inch. Something is very wrong here.