Subscribe to Blog via Email
Good Stats Bad Stats
Search Text
April 2025 S M T W T F S 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 -
Recent Posts
Good Stats Bad Stats
goodstatsbadstats.com
100% refund if no snow
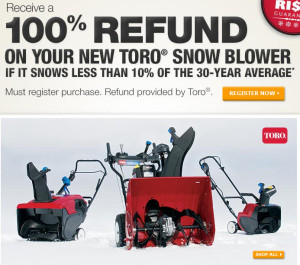 Well not quite if there is no snow. I spotted this at the local Home Depot today and decided to do a little research. Bottom line for me is if I was going to buy a Toro snow-blower I would register to win, but I am not about to buy one because of the “great” deal.
Well not quite if there is no snow. I spotted this at the local Home Depot today and decided to do a little research. Bottom line for me is if I was going to buy a Toro snow-blower I would register to win, but I am not about to buy one because of the “great” deal.
It might sound like a good deal, but it is more like playing the lottery. To determine my odds of winning this lottery I looked up some of the historical snowfall numbers for Washington DC. Those records should be available at the National Climate Center. But earlier this week I was over there looking for some data and found it shut down because of the ineptness of the guys we all elected to govern us. I found the numbers over at Accuweather after a Google search. They are not in a very nice form but can easily be read using R.
Depending on the source the average snowfall in DC is between 14 and 17 inches per year. So to get the 100% refund we would have to get less then about 1.5 inches this winter. It turns out that historically this has happened a total of twice in the last 120 years. Looks like I have something less than a two percent chance of winning.
I did not look at the data for other places but suspect the odds are not much better. In short this is a great deal for Toro if it gets people to buy their brand of snow-blower. I think I would do better to simply wait until late December and buy one on sale.
So if you buy one be sure to register. You might just win. The deal does not appeal to me.
Posted in Telling the Full Story
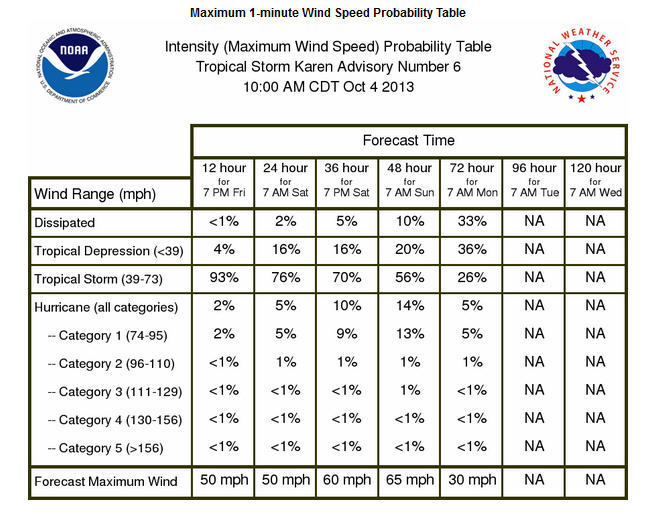
Probabilities for Tropical Storm Karen
I found this a nice table of probabilities that NOAA is putting out for Tropical Storm Karen. It works well as a table. My source for hurricane information is the Hurricane Watch Net that is organized by a group of amateur radio operators as a part of their commitment to provide emergency communication. I’m sure that NOAA has the same information available somewhere. I’ve just found the the Hurricane Watch Net has seemed to package it all very nicely.
Posted in Telling the Full Story
Income inequality measures – Palma vs Gini
I spotted an article and accompanying graphic yesterday on income inequality around the world. The authors chose to use a relatively new measure of inequality called the Palma measure. A quick Google search showed that the push seems to be coming from Alex Cobham and Andy Sumner at the Center for Global Development.
The current discussion may have originated based on a paper that the two recently authored titled: “Is It All About the Tails? The Palma Measure of Income Inequality.” A short youtube clip of Alex Cobham discussing the measure is available and worth a quick listen. Alex does not argue for abandoning the more traditional measure of income inequality, the Gini index, but clearly prefers the Palma measure.
In his arguments Alex makes three points. The first is actually the best of the group. He argues that any measure must be intuitively clear to the users. The Gini in my mind fails this miserably. It is a complex statistic that the “experts” understand. But the general public and the political world likely see it as a number that varies based in income inequality in ways and for reasons that are a complete fog to them. I have never liked the Gini for that reason and because is a statistic that varies so little that most would look at a change in the index and say “so what.”
It is in making his second and third points that Alex’s arguments for the Palma measure fail badly.
What is the Palma measure or as it is sometimes called the Palma ratio? It was proposed by Gabriel Palma. It is simply the ratio of the aggregate income of the top 10 percent of those in the income distribution to the aggregate income of those in the bottom 40 percent of the income distribution. The obvious first question is why should these be the chosen cutoffs? The argument is that the aggregate income of those between these two limits is almost universally 50% of total aggregate income. He argues that is true across counties and across time. As Alex puts it in his second argument all the action is in the tails of the distribution.
It is from that argument that two quick conclusions are made. Neither can be justified. The first is that if all the action is in the tails than one can create a measure that only uses two points on the distribution. Without any justification the issue of what is happening in those tails is ignored.
The second failure is comes from a more complex argument. Alex argues in the video that the Gini index is overly sensitive to the middle of the distribution and therefore is an inappropriate measure. But wait a minute. He just finished arguing that the middle of the distribution does not change across time and country. If the middle of the distribution does not change it does not matter if the Gini is overly sensitive to changes that don’t happen in the real world. He cannot criticize a measure for misbehaving is situations that don’t occur. He is saying because the center of the distribution does not vary the Palma measure is a good measure, but because the Gini is sensitive to changes there the Gini is a bad measure. The real conclusion should be that if the center of the distribution does not vary then both measures are good unless there are other reasons to disqualify one of both of the measures. If the center of the income distribution does vary then he must conclude that neither measure is very good. In that case the Gini is overly sensitive and the Palma ignores what is going on there.
Alex’s summarizes his third point in the video by saying that the Gini index does not give you what you think it does. This is a more complex argument and fails for two reasons. His description of what the Gini looks like is given in what appears to be a guest post in Duncan Green’s From Poverty to Power blog.e There he claims that the Gini is:
Gini = (0.581 * income share of top 10%) – (1.195 * income share of bottom 40%) + 0.419
And he follows up saying “how intuitive is that?” It took some work to figure out where the equation came from. It is in the paper he references in the post titled: “Is It All About the Tails? The Palma Measure of Income Inequality.” The description is on page 23 table 7. What he did was to run an ordinary least squares regression using data from the World Bank. The independent variables are the income share of the top 10 percent and the income share of the bottom 40%. The dependent variable is the Gini index. The equation above is the fitted regression model.
Of course this model is not intuitive. It is not the model this is the basis for the Gini index. It is a model created by the authors. No matter what the coefficients of the model turned out to be and no matter how good the data fit the model the model would never be intuitive. Arguing that it should be intuitive is just nonsense.
The strength of his argument comes from the observation that the achieved and adjusted R-square of 1.000 for the fit using 826 observations. However, given the nature of the Lorenz curve the is underlying model for the Gini index a reasonably good fit for the regression was inevitable. The regression attempts to estimate the area between a diagonal line from (0,0) to (1,1) and the Lorenz curve based on the location of two points on the Lorenz curve.
At this point Alex caps off his argument saying that the Gini index does not give you what you think you are getting. It is in fact based on no more data than is the Palma measure. He says that based on the results of his regression.
So let’s assume his regression is a good fit to what is going on with the Gini index. Now tie that in with the argument that the share of income by those between the 40 percentile and 90 percentile is extremely stable at 50 percent. An interesting result then emerges. If the claim that the 40 to 90 percent group consistently accounts for 50 percent of aggregate income is true the share taken by the top 10 percent is 50 percent minus the share taken by the bottom 40 percent. This then fixes the relationship between the two numbers used to compute the Palma index and the two numbers in his model for the Gini index. In short the Palma measure and the Gini index based on his regression model can be fully determined exclusively by the share of income of the top 10 percent. And in addition since both measures are monotonically increasing as the share of income of the top 10 percent increases there is a one-to-one correspondence between the Palma measure and the Gini index. The only difference is in how they respond to change in the share of income of the top 10 percent. If I know the Palma measure then I know the Gini index and vice-verse.
Just to be extra clear in this situation we have under his model and assumption that the middle group (the 40-90 percentile group) consistently claims 50 of the income share:
Palma = (income share of top 10%)/(50 – income share of top 10%)
and
Gini = (0.581 * income share of top 10%) – (1.195 * (50 – income share of top 10%)) + 0.419
Left to the reader is the exercise of making the plot of Palma vs Gini as a function of the income share of the top 10%.
Posted in Methodolgy Issues, Telling the Full Story