Death and the Emerald Ash Borer

In January of this year the US Forest Service published a paper titled: “The Relationship Between Trees and Human Health” in the American Journal of Preventive Medicine. The paper reported on an association between deaths from from heart disease and lower respiratory track disease and deforestation caused by the Emerald Ash Borer.

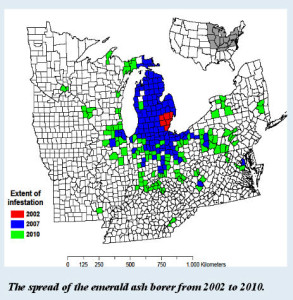The authors go to great lengths to cite from the literature the health benefits of a natural environment. The thesis they present is that seeing the death of the Ash trees somehow creates a stress, or a lack of nature in a person’s environment that leads to an increase in the mortality rate. They use data from fifteen states where the Emerald Ash Borer has been seen. I have copied their county level map showing the extent of the infestation on the right. The infestation started in the Detroit area in 2002 and has slowly spread from there.

The model the authors use is a very simple linear regression. They include a number of variables on demographics, length of the infestation, and time series data on the growth and extent of the infestation. They also include data on the amount of tree cover from the Ash trees. Wisely they included a trend variable to account for improvements in hearth outcomes over time. A variable that seems obvious but is not mentioned it overall tree cover. If the argument is that the visual decline in tree cover is a stress then it seems clear that a measure of the magnitude of such a decline is essential to the analysis, but for some reason they choose only to include in the model tree cover from the Ash and not the decline in total tree cover due to the infestation. Their apparent decision not to include total tree cover in the model is puzzling as the authors used the variable to derive the estimates of Ash tree cover in each county.

Another problem that the authors faced was they were trying to identify a small effect relative to the amount of data available. In the regression the coefficient for the Emerald Ash Borer was barely statistically significant while the associated confidence interval was very large. For example in the regression for Heart disease the 90 percent confidence interval extended from -25.38 to -1.64. Keeping in mind that variance estimate are always less reliable than the quantity being estimated an interval of this size is not something I would want to base claims upon. This is the danger of using standard statistical testing and failing to pay proper attention to what the data is capable of showing.

The authors discuss briefly a third regression they ran. For this final regression they used the same models to predict accidental deaths. This model did not result in a statistically significant regression coefficient for the impact of the Emerald Ash Borer. From this the authors drew comfort that their model worked well in that it showed no statistically significant effect for a cause of death that would have no “plausible” link to the Emerald Ash Borer. But in reality this regression provides not information. The fundamental reason is that the Heart Disease it the leading cause of death, respiratory track disease ranks third, while accidental death ranks fourth. With fewer deaths it is less likely that the results of their model would indicate a statistically significant result. This is particularly true given the large confidence intervals they saw in their original models. This is also the wrong approach to the question. The appropriate test is a formal comparison of the models. Test for example the difference between the regression coefficients for the Emerald Ash Borer variable in the three models. Comparing statistical significance to lack of statistical significant is a common but wrong approach. Formal testing is required.

I have to wonder as well why the authors choose to look at accidental deaths for their third model rather than cancer deaths as the number of cancer deaths is much larger than those from accidents being the second leading cause of death in the US.

Also fundamental to this type of analysis is the question as to the appropriateness of a linear model. Why should we assume a linear relationship between the variables in the model. That relationship is assumed. A model is fit. The results are reported. But there is nothing reported on why a linear relationship is appropriate.

The underlying model of what is happening is not well specified. Is the loss of the trees hastening deaths that would have occurred anyway? In that case the effect in the model is temporary as the pool of those that would be impacted is depleted by the earlier than normal deaths. That is not reflected in the model. It is hard to envision other models. I don’t think a claim that the presence of the Emerald Ash Borer causes heart disease is something the authors would want to entertain. And certainly it is doubtful as relevant in the short time frame since the original infestation by the borer.